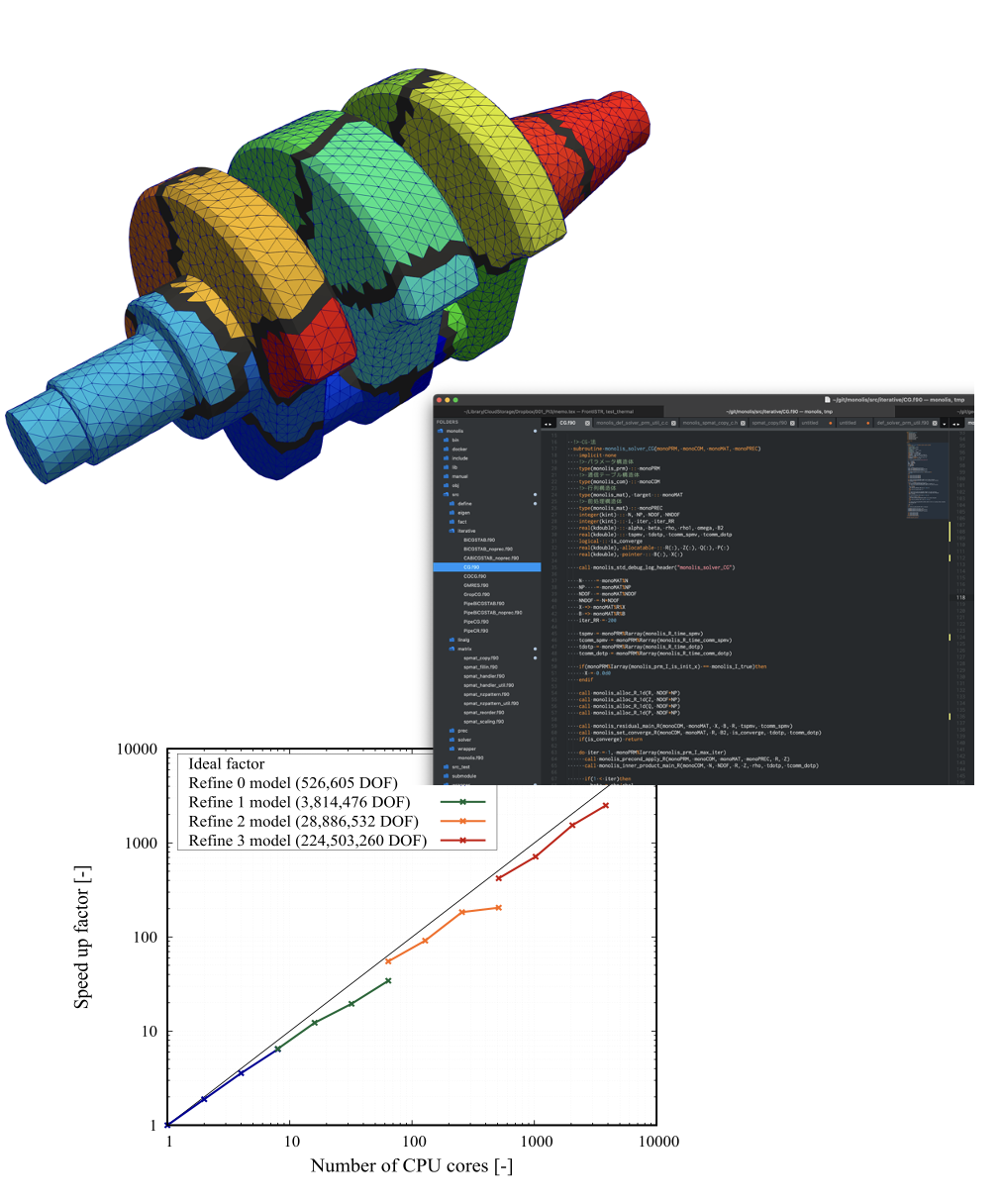
数値シミュレーションの大規模並列計算

森田研究室では「工学分野に起因する解きにくい問題」を対象として、数値解法・並列解析システムに関する研究を遂行します。

我々の身の回りには、固体の変形、流体の流れ、熱など様々な現象が満ちあふれています。これらの現象は、我々が数理として取り扱えるよう様々なモデル化が施され、支配方程式という形で記述されます。支配方程式の解を得ることができれば、私達は現象を理解し予測することができます。一方、その多くは微分方程式で記述されており、解析的に解ける例はほとんどありません。そこで支配方程式を計算機上で表現できるよう離散化して数値的に解を得る手段、つまり数値解析の出番となります。

解析対象の支配方程式を離散化すると、以下のように、しばしば解きにくい問題に直面します。

これらの問題は汎用的な解法・解析システムが利用できない場合が多く、それゆえ非常に興味深い研究対象となります。 本研究室では、解析対象となる学問領域の深い知識・専門性と数値解法・並列計算技術を組み合わせた解決を目指します。