【基盤技術構築】「グラフ的視点」によるマルチフィジックス解析・データ分散型並列解析の一般化

[Fundamental Technology] Generalization of Multi-Physics and Data-Distributed Parallel Analyses from a "Graph-Based Perspective"

研究概要

背景・動機：

数値解析や力学シミュレーションが発達している昨今、対象とする問題は年々複雑化しており、その複雑問題を解析するためのプログラムも複雑化の一途を辿っています。これはあくまで大学の教育現場の視点になりますが、こういった問題を対象とした数値解析戦略の研究を実施しようとすると、プログラムの煩雑性がボトルネックとなり、修士学生の2年間ではまともに研究が成り行かない、といった事態が起きています。そこで我々は、マルチフィジックス解析 (複数の物理現象が相互作用する複雑な現象に対する解析) やデータ分散型並列解析 (スーパーコンピュータなどを使用した並列解析) などの実装面で時間的コストがかかる対象に対し、計算点の相互作用をグラフとして記述できる事実に着目し、あらゆる数値解析手法を包括した一般的方法論とその可搬性の高いライブラリの開発を進めています。

計算点相互作用・疎行列構造・グラフ：

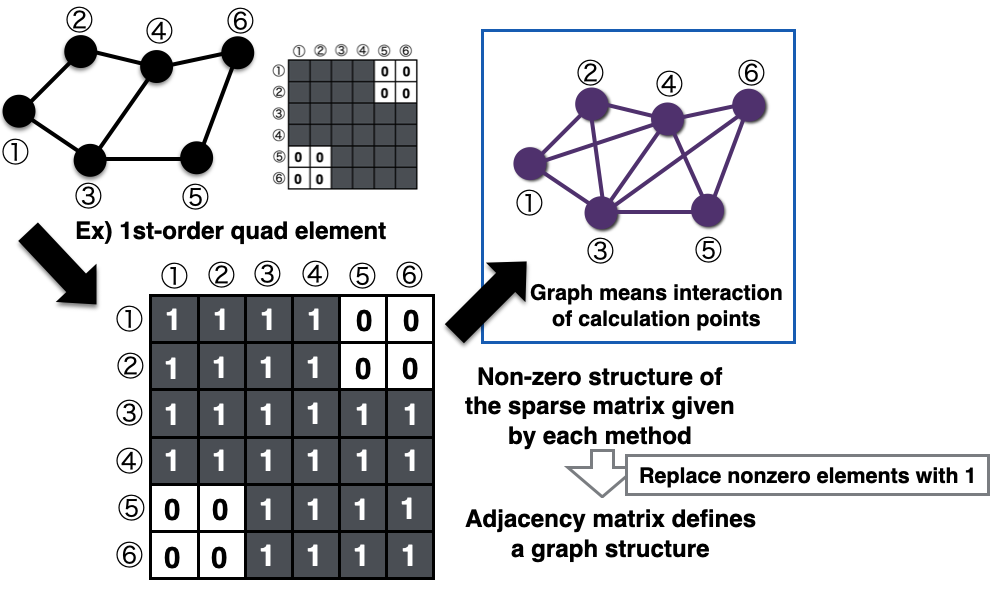
数値解析手法は、各手法固有の「計算点の相互作用」 (微分等の演算子の計算方法) を持っています。また、すべての数値解析手法は最終的に連立一次方程式 (行列) に帰着します。(※ 非線形問題の場合は、Newton-Raphson 法などの非線形解法を適用した接線行列がこれに相当します。また、陽解法ではそうならない、という主張がありますが、「行列がたまたま対角行列である場合」と考えられます。)

この「計算点の相互作用」によって行列の疎構造 (どこに値が入り得て、どこが0であるか) が決定され、この行列をグラフ理論における隣接行列に変換することで、任意の数値解析の系を一意にグラフへと変換できます。

重み付きグラフ分割と幾何学的領域分割：

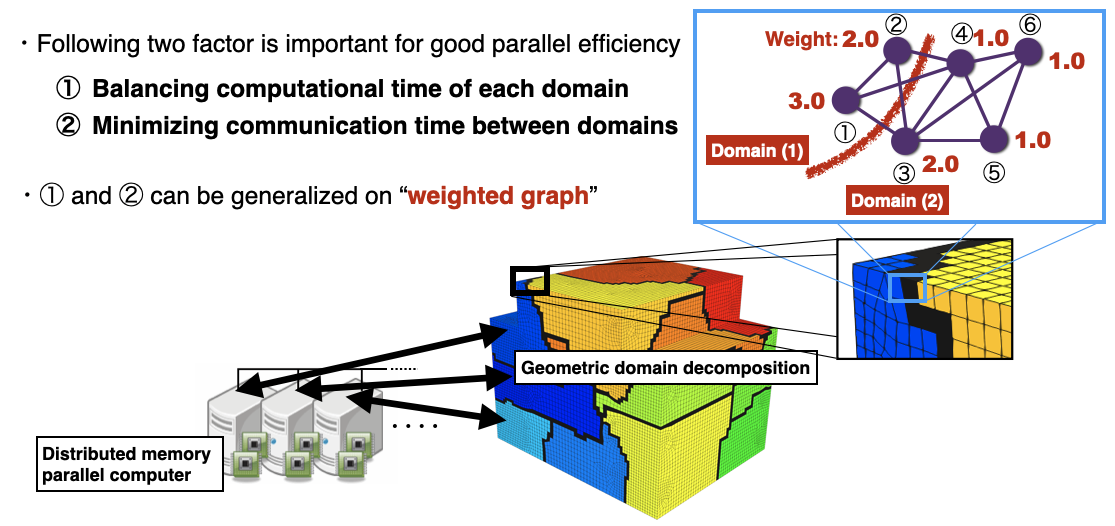
前述のグラフに対し、各計算点ごとの計算時間や計算機間の通信時間などを重みとして設定することで重み付きグラフが定義できます。これに対して、何らか制約 (例: 並列計算であれば各領域の計算時間を均等にしたいので、各領域内の計算点の重みの合計 = 各領域の計算時間　を均等にするような制約) をもとにグラフを分割します。結果的に、計算点は空間的にグループ化された「領域」となり、領域分割がなされます。我々は、これらのグラフに関する演算と領域分割操作を、ライブラリ Gedatsu (graphs with embedded data subdicision utilities) としてまとめ、公開しています。

領域分割された系に対する並列連立一次方程式求解：

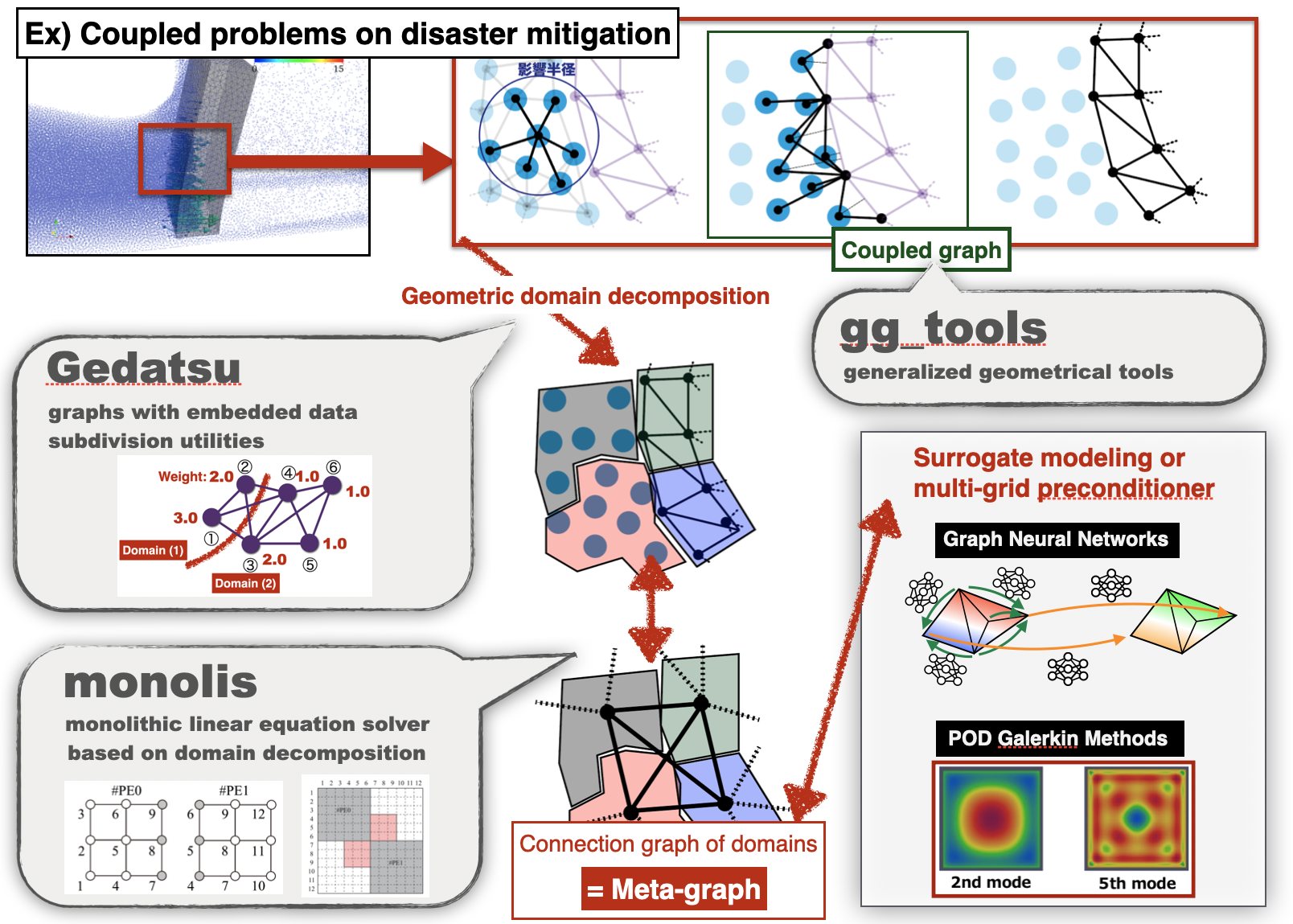
我々は、この領域分割された系に対し、連立一次方程式を並列に効率良く求解するためのライブラリ monolis (monolithic linear equation solver based on domain decomposition) を開発しています。また、分割された領域の隣接関係を表す「メタグラフ」構造を利用し、マルチグリッド的前処理の開発も実施しています。

マルチメソッド・マルチフィジックス解析等、複雑な系への適用：

上記のように、グラフで一般化された考え方に従うと、異なる数値解析手法どうしや、異なる力学現象どうしを連結させた複雑な系の解析もシンプルな形に一般化できます。図では、粒子法流体解析と有限要素法構造解析を連結した流体構造連成解析の例を紹介していますが、このような問題も、「各手法・各現象ごとの計算点グラフ」と、「各手法・各現象どうしをつなぐ連結グラフ (coupled graph)」を考え、それらを統合することでシンプルに扱うことができます。

この連結グラフを作成する際、幾何学的な内外判定や距離計算が必要となるため、領域分割型並列計算環境で動作する一般化幾何計算ライブラリ gg_tools (generalized geometrical tools) の開発を行っています。

様々な発展的数値解析手法への適用例：

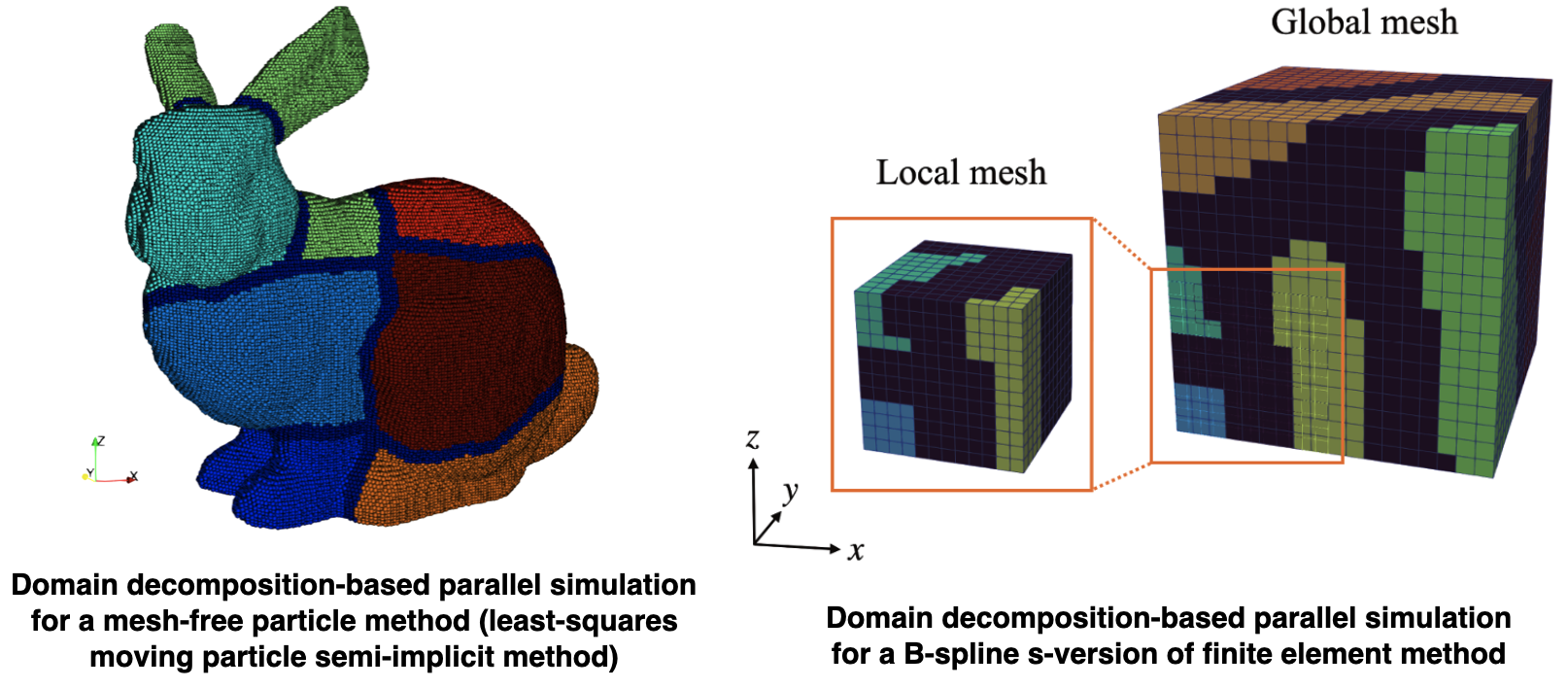
このようなグラフを用いた領域分割は、主に有限要素法並列解析の分野で広く利用されていましたが、我々は上記のライブラリを利活用し、有限要素法以外の発展的な数値解析手法に適用しています。

共同研究者・共同研究機関

筑波大学森田直樹研究室

Research Overview

Background and Motivation:

With the recent development of numerical analysis and computational mechanics, the target problems are becoming more and more complex, and the programs to analyze these complex problems are also becoming more and more complicated. This is only from the viewpoint of university education, but the complexity of the program is a bottleneck when trying to conduct research on numerical analysis strategies for such problems, and the research cannot be completed in two years by master students. Therefore, we have focused on the fact that the interaction of computational points can be described as a graph, which is time-consuming in terms of implementation, such as multi-physics analysis (analysis of complex phenomena in which multiple physical phenomena interact) and data-distributed parallel analysis (parallel analysis using supercomputers, etc.), We are developing a general methodology that encompasses all numerical analysis methods and a highly portable library of such methods.

Interactions of Calculation points, Structure of Coarse Matrix, and Graph:

Each numerical analysis method has its own "computational point interaction" (how operators such as derivatives are computed). In addition, all numerical methods ultimately result in a linear system of equations (matrices). (* For nonlinear problems, this corresponds to a tangent matrix to which a nonlinear solution method such as the Newton-Raphson method is applied. There is also the claim that this is not the case with explicit solution methods, but this is considered to be "the matrix is a diagonal matrix in this case.")

This "interaction of computation points" determines the sparse structure of the matrix (where values can be entered and where values are zero), and by transforming this matrix into the adjacency matrix in graph theory, we can uniquely transform any system of numerical analysis into a graph.

Weighted Graphs and Geometric Domain Decomposition:

A weighted graph can be defined by setting the computation time for each computation point and the communication time between computers as weights for the aforementioned graph. In contrast, the graph is partitioned based on some constraint (e.g., for parallel computation, the computation time in each subdomain should be equalized, so we can set a constraint to equalize the sum of the weights of the computation points in each region (= computation time) in each region). As a result, the computation points are spatially grouped into "subdomains." We have compiled and release these graph-related operations and domain partitioning operations in the library "Gedatsu" (graphs with embedded data subdicision utilities).

Parallel Solvers for Linear Equations for Domain Decomposed systems:

We are developing "monolis" (monolithic linear equation solver based on domain decomposition), a library for efficiently solving simultaneous linear equations in parallel for this domain decomposed system. We are also developing a multigrid-like preprocessor using a "metagraph" structure that represents the adjacency relations among the decomposed domains.

Application to Complex Systems Such as Multi-method and Multi-physics Analysis：

From the viewpoint of the above graph generalization, analysis of complex systems that are coupled with different numerical methods or different physical phenomena can also be generalized to a simple form. The figure shows an example of fluid-structure interaction analysis in which a particle method for fluid analysis is coupled with a finite element method for structural analysis. The coupled graphs can be integrated to simplify the problem.

Since geometric inner/outer and distance calculations are required to create these coupled graphs, we have been developing gg_tools (generalized geometrical tools), a generalized geometrical calculation library that works in a domain decomposition-type parallel computing environment.

Examples of Application to Various Advanced Numerical Methods:

Although domain decomposition using such graphs has been widely used mainly in the field of finite element parallel analysis, we have taken advantage of the above library and applied it to advanced numerical methods other than the finite element method.

Collaborators

Prof. Naoki Morita, University of Tsukuba, Japan

三目研究室【基盤技術構築】「グラフ的視点」によるマルチフィジックス解析・データ分散型並列解析の一般化

三目研究室