科学研究費補助金  国際共同研究加速基金(国際共同研究強化(B)) 課題番号18KK0115  

ミクロ可視化実験および粒子ベース解析による複雑粒状体統計力学理論の探求

●研究代表者：

松島 亘志(筑波大学システム情報系)

●研究分担者：

高野 大樹 (国立研究開発法人海上・港湾・航空技術研究所, 港湾空港技術研究所)

渡邊 保貴 （ 一般財団法人電力中央研究所, サステナブルシステム研究本部）

●国際研究協力者：

Raphael Blumenfeld (University of Cambridge, Imperial College London)

Cino Viggiani (Laboratoire 3SR, Universite Grenoble Alps)

Eddy Ando (Laboratoire 3SR, Universite Grenoble Alps)


●科研ウェブサイト：

KAKEN

●研究の背景：

1.1 土質力学・地盤工学的背景
地盤材料は自然の材料であり，我々はその上に住み，それを利用して生活している．地盤材料をより安全に，より効率的に利用するためには，その力学特性を精度良く予測する必要がある．これまで主流の地盤の材料力学モデルは，金属材料の現象論的構成モデルを修正したもの（Drucker-PragerモデルやCam-clayモデル，最近では上下負荷面モデルなど）であり，粒度の揃った砂，再構成粘土などの比較的単純な地盤材料に対する比較的単純な条件下での応答であれば，要素実験により適切にパラメータを決めることで再現可能であり，多くの応用事例がある．一方で，良配合材料，破砕性材料，固着材料など，より複雑な材料に対して，また低固相率状態から高濃度状態への遷移や長期挙動などの，複雑な条件下での応答に関しては，予測精度の低下や，そもそも適切な条件での要素試験が実施できないため，応答を予測できないのが現状である．特に外的な条件によって材料物性が変化していく場合は，上述のモデルではパラメータの進化則を決めるのが非常に困難となる．
もともと地盤材料は土粒子の集合体であり，材料物性の変化は，粒子物性(粒度分布や粒子形状など)及び粒子間相互作用(粒子接触点でのセメンテーション(固着)やvan der　Waals力など)の変化が原因となっている．ここで重要なのは，このような粒子スケールの現象自体は，比較的単純な法則で記述できる，ということである．すなわち，粒子物性から組み上げた力学モデル(微視力学モデル)を構築すれば，巨視的挙動に粒子物性の変化を自然に取り込むことができると期待される．
そのような観点から，現在までにいくつかの微視力学モデルの枠組みが提案されているが，どれも十分な成果を挙げていない．その突破口として本研究プロジェクトで注目しているのが，(a)微視的な粒子構造が，ランダムでありながら，何らかの法則に基づいて決まっているようであること，(b)コロイドのような固相率が非常に小さい系から，ぎっしり粒子が詰まった系までを統一的に扱える微視構造モデルの枠組みが徐々に整いつつあること，という２点である．特に(b)は，粘土・砂・軟岩といった材料の違いや，固体的な挙動から流体的な挙動までを統一的に扱えるモデルの開発につながるものである．このモデル構築の鍵となる力学理論が統計力学である．

1.2 物理学的背景
19世紀末から20世紀初頭にかけて確立された統計力学は，熱力学やソフトマターの分野では大きな成果を挙げたが，20世紀後半になって適用を試みられた粒状体(砂や粉などの固体粒子の集合体)では未だ十分な成功を収めたとは言いがたい．特に粒子がぎっしりつまった系では，粒子運動の擾乱や粒子自体の熱的振動も無視できるため，熱統計力学のように運動量を状態量として取ることはできない．その代わりに接触力を状態量として圧力と関連づけるのが自然であるが，接触力分布は，粒状体の微視構造の影響と切り離すことはできない．そのため，微視構造のばらつきを表現する何らかの指標の提案と，それと接触力分布との関係を定式化する必要がある．
　これらについての理論的研究が基礎物理学の分野で進んでいるが，未だ状態量の性質を様々な条件下で調べているという段階である．その中で，Matsushima & Blumenfeld [1,2]は，極単純な２次元粒状体の微視構造の安定性の概念の有効性を示した．また，Suzuki & Matsushima [3]は，粘土のような粒子間引力のある系では，粒子間引力(内力)と外力との比によって，微視構造の性質が遷移することを見いだした．一方，Blumenfeld et al. [4]は，微視構造と接触力の両方を，相関のある状態量として取り扱う統計力学的枠組みを示している．


●研究の目的：

以上の背景を元に，本研究課題では，地盤材料の力学特性についての，以下のような地盤工学における核心的「問い」に答えることを最終目的とする．
(1) 粘土と砂は何が違うのか？　→粘土・砂・軟岩までを統一的に扱えるモデルの開発
(2) 地盤材料の塑性圧縮とは何か？→粒子破砕と微視構造破壊を統一的に扱えるモデルの開発
(3) 塑性圧縮時の圧力と間隙率の関係式の起源は？→微視的物理量から巨視的物理量を導く
(4) (塑性)圧縮指数と粘着力の関係は？ →巨視的物性値間の関係を微視モデルより導く
(5) 統計力学は運動量を状態量としない静力学的枠組みに対して適用できるのか？


●研究の方法：

本研究では，高解像度のx線μCT装置から得られる３次元粒子堆積構造情報を，最新のアルゴリズムで解析し，統計力学理論に必要な状態量を取得する．また粘土など数μm以下の粒子材料に関しては，湿潤状態（すなわち，粘土の自然状態）の観察が可能な低真空SEMを用いる．いずれの手法でも，低固相率から高固相率への堆積試験や，試験体に載荷や熱化学反応などの外的作用を加えた場合の材料変化を観測する．特に，３次元粒子堆積構造に関しては，粒子形状が及ぼす影響の検討を系統的に行うため，3Dプリンターを用いて，様々な細長度および扁平度の楕円体粒子を多数作成し，それらの堆積実験や載荷実験を行うことで，粒子形状が堆積構造に及ぼす影響，そしてそれが全体としての力学特性に及ぼす影響について検討を行う．
一方，数値解析では，基礎的な堆積構造を検討する２次元円形／楕円形粒子を用いた個別要素法(Discrete Element Method; 以下DEM)の解析に加えて，複雑粒子形状や粒子破砕／磨耗，任意の相互作用を表現できるLS-DEM(レベルセット個別要素法)[5]を用いて，実験では取得困難な粒子間力と局所微視構造の関係などの情報を取得する．
　また，本研究は国際共同研究加速基金によるプロジェクトであり，海外の研究者との共同研究が，研究遂行の鍵となっている．フランスのグルノーブル・アルプス大学3SR研究所は，地盤材料のx線μCT実験で世界のトップを走る研究所であり，そこで3Dプリンターを用いた堆積／載荷実験の共同研究を行う．一方，ケンブリッジ大学／インペリアルカレッジロンドンのBlumenfeld教授は，粒状体の統計力学の専門家であり，統計力学理論の構築についての共同研究を実施する．
共同研究の実施体制を図1に示す．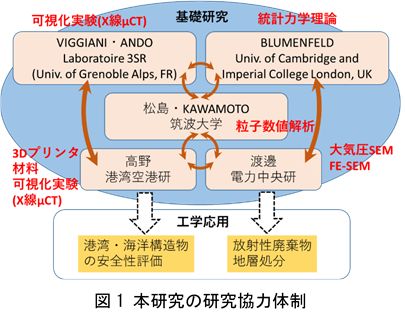


●研究成果：

　本プロジェクトの遂行においては，研究担当者間の連絡を緊密に行い，必要な方向修正等を行いながら進めた．特に新型コロナ感染症の影響は甚大で，予定していた渡航がキャンセルされたことで，実験の遂行などに影響が出た．１年目は予定通り3SR研究所における共同研究が実施され，3Dプリンター粒子の設計と材料共有が行われたが，２年目は2020年3月に予定していた渡航をキャンセルせざるを得ず，３年目も同様で，別々に実験を実施して，その結果をオンラインで共有する，という形で共同研究を実施した．そのような状況ではあったが，全体としては以下に示すような，十分な成果を上げることができた．
(1) 不規則３次元形状を定量評価する力学ベースの形状指標の提案[6]
x線μCTによって取得された不規則形状の砂粒子を用いたLS-DEM載荷実験の解析を行い，個々の粒子形状情報のみから得られるパラメータであるα_pと，粒状体中の接触点情報より得られるα_cの平均値がほぼ一致することを見いだし，α_cがせん断を受ける粒状体中での粒子回転のばらつきを抑え，接触点でのモーメント抵抗によってせん断抵抗を増加させるメカニズムを示した(図2)．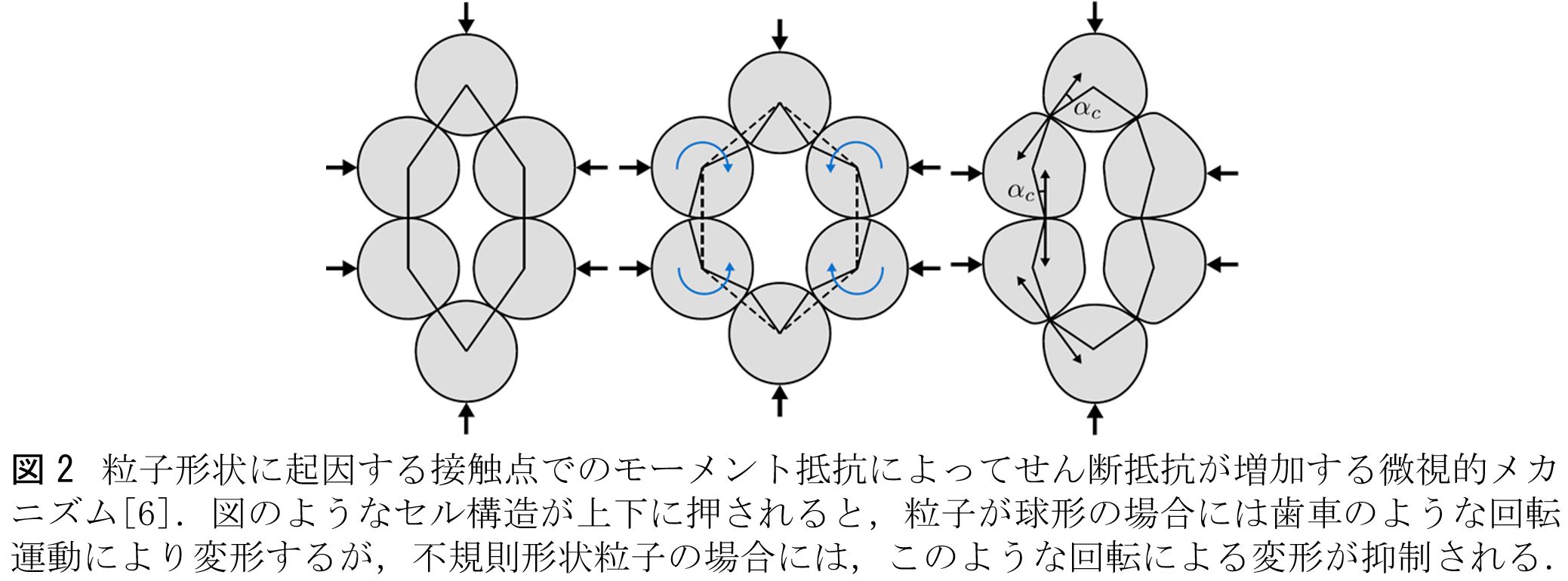


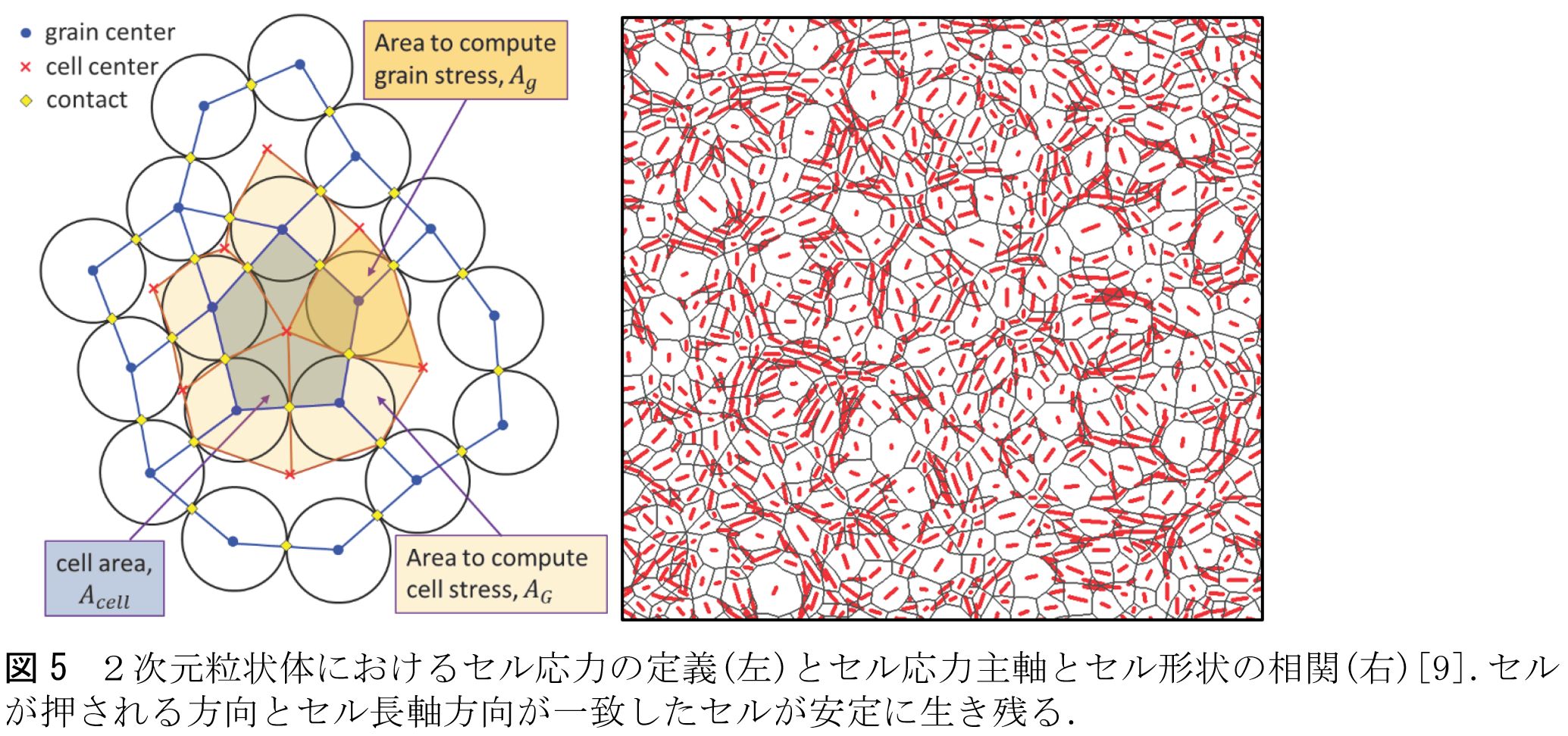
(2) 微粒子凝集実験および2次元DEM解析による凝集体形状特性の検討[7]
人工球形粒子および２種類の粘土(カオリナイトおよびベントナイト)の凝集実験および２次元個別要素法解析によって，粒子間引力と粒子間摩擦力の２つの微視的物性値が凝集体形状に及ぼす影響を明らかにした(図3)．


(3) 楕円形粒子の堆積構造における形状に起因した結晶化現象の検討[8]
2次元個別要素法を用いて，楕円形粒子の堆積構造に関する基礎的検討を行った．特に隣り合う粒子の長軸が同じ方向に揃う結晶化現象について，その統計的な性質と間隙セル構造に及ぼす影響を明らかにした(図4)．


(4) ２次元粒状体のセル応力の検討[9]
2次元粒状体の間隙セル構造に作用するセル応力についての統計的性質について検討し，バルク応力や降伏基準との関連性を明らかにした．また，せん断を受ける粒状体中の間隙セルの離散集合について，発展方程式による理論解析を行い，個別要素法結果と比較して，そのメカニズムの考察を行った(図5)．


(5) 応力発光粒子を用いた粒状体応力伝播の可視化と計測[10]
応力発光材を塗布した円柱粒子を用いた載荷試験を行い，２次元粒状体中の応力伝播を可視化し，接触力の計測を行う手法を開発した(図6)．


(6) 細長度，扁平度の異なる楕円体粒子の堆積構造と力学挙動の把握
3Dプリンタで異なる細長度，扁平度の人工粒子を作製した．異なる堆積方法で作製した供試体をX線CTにより可視化することで，粒子形状が堆積構造に及ぼす影響について検討した．より粒子形状が扁平になるほど粒子の配向はばらつきが小さくなることが確認できた．三軸試験の結果，せん断時の変形挙動は粒子形状が扁平なほどダイレイタンシーによる体積変化が小さく，一次元圧密に近い挙動が確認できた．(発表準備中)
(7) 電子顕微鏡による粘土凝集体の液中挙動の観察手法の開発
電子顕微鏡による液中観察により、粘土の凝集体同士が一定以上の距離を保って運動する様子を捉えた。また、粒度試験を通じて、一次凝集での寸法や形状が擾乱に対してより安定的であることが示唆された。より大きな凝集体についても、せん断変形では力学的役割を担うことが顕微鏡下での無拘束せん断により示唆された。（発表準備中）
(8) x線μCTによる地盤材料の可視化実験の後処理プログラムプラットフォームの開発[11]
x線μCTによって得られる大量のデータから，地盤材料の力学に必要な微視情報を取得するために必要な，後処理プログラムのプラットフォームを開発した．

上述の成果をベースに，今後は以下のような課題に取り組む予定である．
・数値解析で示された粒状体内のセル応力の考え方について，応力発光粒子可視化実験などで検証する．
・数値解析で示された楕円形粒子の堆積構造について，x線μCT等の可視化実験により検証する．
・粘土粒子の凝集体のせん断挙動について，数値解析と可視化実験の両面から検証する．特に非粘着性粒子で観測されたセル構造や楕円形の結晶構造などについて詳細に検討し，塑性圧縮のミクロなメカニズムの解明につなげる．
・３次元セル構造の同定手法を開発し，それを媒介とした統計力学理論の構築を目指す．

●参考文献：

[1] Matsushima, T., Blumenfeld, R., Universal Structural Characteristics of Planar Granular Packs, Physical Review Letters, 112(9), 098003, 2014.

[2] Matsushima, T., Blumenfeld, R. (2017). Fundamental structural characteristics of planar granular assemblies: Self-organization and scaling away friction and initial state. Physical Review E, 95(3), 032905.

[3] Suzuki, A., Matsushima, T., Meso-scale structural characteristics of clay deposit studied by 2D Discrete Element Method, Proc. IS-Cambridge, Geomechanics from Micro to Macro, Soga et al. Eds, Taylor & Francis, ISBN 978-1-138-02707-7, 33-40, 2014.

[4] Blumenfeld, R., Edwards, S. F., On granular stress statistics: Compactivity, angoricity, and some open issues. The Journal of Physical Chemistry B, 113(12), 3981-3987, 2009.

[5] Kawamoto, R., Ando, E., Viggiani, G., Andrade, J. E., Level set discrete element method for three-dimensional computations with triaxial case study. Journal of the Mechanics and Physics of Solids, 91, 1-13, 2016.

[6] Kawamoto, R., Andrade, J., Matsushima, T., A 3-D mechanics-based particle shape index for granular materials. Mechanics Research Communications, 92, 67-73, 2018.

[7] 瀬口拓遼, 松島亘志 (2018) 人工球形粒子および粘土粒子の凝集体形状分析とDEM解析，土木学会論文集A2(応用力学), 74, 2, I_411-I_420.

[8] Jiang, X., Matsushima, T., Blumenfeld, R., Structural characteristics of ordered clusters in packs of ellipses, Proc. Powders and Grains 2021, 06004, 4p. doi.org/10.1051/epjconf/ 202124906002, 2021.

[9] Matsushima, T., Blumenfeld, R. Statistical properties of cell stresses in 2D granular solids, Proc. Powders and Grains 2021, 02006, 4p., doi.org/10.1051/epjconf/202124902006, 2021.

[10] Kondo, A., Takano, D., Kohama, E., Bathurst, R. J., Visualization and measurement of load transmission in granular assemblies using mechanoluminescent-coated particles. Granular Matter, 21(3), 1-12, 2019.

[11] Stamati et al., spam: Software for Practical Analysis of Materials. Journal of Open Source Software, 5(51), 2286, https://doi.org/10.21105/joss.02286, 2020.