研究概要

研究概要

並列的解法を用いた可変形態リンク系のフィードフォワード制御

1. 緒言

ロボットを構成する重要なメカニズムの一つであるリンク機構に対し，動的な影響を考慮したトルクを算出するためには，その系に応じた動力学方程式を導出し，目標軌道から逆動力学計算を行う必要がある．旧来より用いられる動力学方程式は，一般的に相対的な回転座標系に基づき力学的な作用関係がすでに式中に含まれた形で導出されるため，リンク系の結合条件や拘束条件が変化した場合，式の再導出が必要となる．特に，系内に閉ループ系が形成された途端にその導出は困難となり，様々な工夫が必要となる[1][2]．しかし，ロボットの動作が多様化すると開・閉ループ系が高速に切り替わる，あるいは混在するといった状況が発生し，逆動力学の計算がますます困難となることが予想される．そこで，リンク機構の形態に依らない統一的な解法を開発することを目的とし，有限要素法(FEM)を用いた並列的逆動力学計算法が考案された[3]．

本解法は，様々な形態のリンク系に適用できる柔軟性を有する一方で，解の算出方法や扱う座標系などが従来の方法とは異なるため，実際に制を行う上で重要となるフィードバックの導入や，解の算出時間などについて検討を行う必要がある．そこで本報告では，並列的逆動力学計算法の有効性を検証するため，これを導入したフィードフォワード制御系を構築し，まずシステム内でトルク計算に要する時間などについて検証した．次に，本手法の利点である並列性および柔軟性を確認するため，形態が連続的に変化するリンク系に対する制御実験を行った．

2. 並列的逆動力学計算法の計算精度

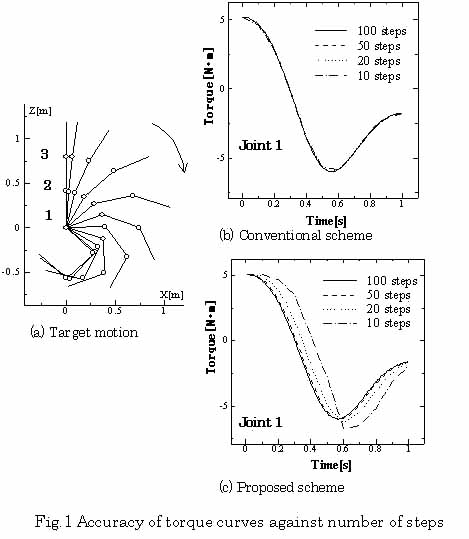
本解法では，トルクの次元の動力学方程式を厳密に解くのではなく，力の次元の運動方程式を増分的に解き，これを足し合わせた近似解（節点力）をトルクに換算する点が，従来の解法とは大きく異なる点である．そこで，並列的解法により得られる近似解の精度，および十分な精度を得るために必要なステップ数などの検証が必要である．図1に，3リンク機構のトルクを従来の動力学方程式によって求めた結果，および並列的解法で計算した結果を示す．厳密解を算出する従来の方法ではステップ数により解の精度は落ちないが，近似解を算出する並列的解法では，解の精度がステップ数に依存することが分かる．ただし，1sの動作時間に対し50～100ステップ以上を確保すれば，実用上十分な精度のトルク曲線が得られることが確認できる．これは，例えばサンプリングタイムを10msとした場合に，十分な精度が保証されることを意味する．

3. 形態可変リンク系のフィードフォワード制御実験

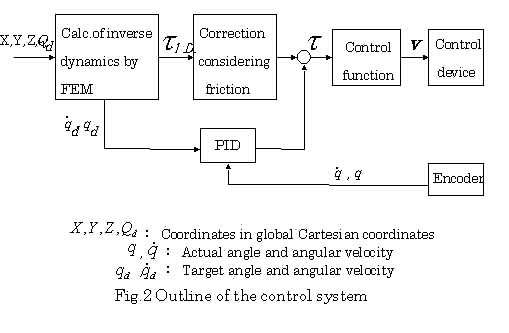
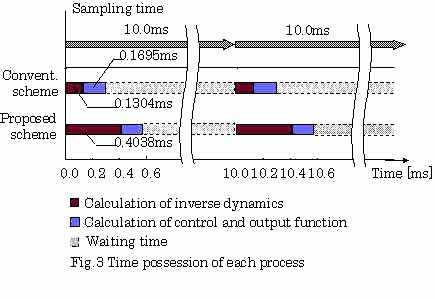
本解法を用いて構築した制御系の全体の構成は，図2のようになる．直交座標系に基づく全体座標系での目標軌道を入力とし，FEM による逆動力学計算を経て，逐次的に全リンクのトルクτ_I.D.が算出される．これにモータを駆動する際の慣性力および動摩擦力，そしてPIDフィードバック値を足し合わせ，最終的な制御トルクτが出力される．従来の手法と本解法の計算時間を比較するため，例として４リンク系を制御する過程中の各プロセスの占有時間を図3に示す．ここでは，サンプリングタイムを10msとした．制御過程は主に逆動力学計算部と制御・出力関数計算部の2つのプロセスから成り，前者は当然解法によって異なるが，後者は共通のプロセスとなる．図から分かるように，逆動力学計算部で本解法は従来の手法より３倍程度の計算時間がかかるが，サンプリングタイムと比較すると十分に短く，実用的な観点からは問題ないといえる．

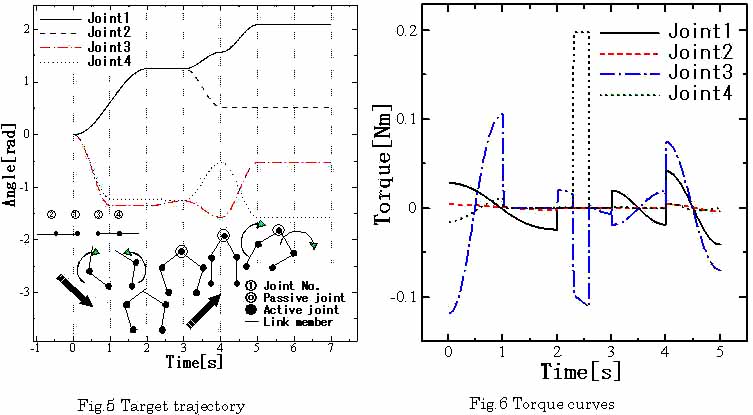
　次に，開リンク系から閉リンク系へと連続的に形態を変化させる機構に対し，軌道追従制御実験を行った．本実験で用いたリンク機構の概観を図4に示す．逆動力学の影響を顕著にするため，各モータにはギアを介していない．また，2本の開リンク系の先端に配置した拘束機構を連結することで，閉リンク系を構成させることが可能となっている．拘束機構は並進方向の動きを拘束し，ピン状態の受動関節となる．本実験で設定した目標軌道を図5に示す．動作開始後3秒間は2本の独立した開リンク系として動作し，3秒後に両者の先端が拘束され，その後は1つの閉リンク系として動作する．この際，リンク系の境界条件が変化するにも関わらず，本解法では連続的にトルク値の計算が行われる．算出されたトルク曲線を図6に示す．2.3s～2.6sの間に大きめのトルク値が算出されているのは，拘束機構にはめ込むのに余剰な外力が必要となり，意図的にトルクを発生させているためである．具体的には，関節3,4に並進方向の力を発生させている．本解法では力の次元で方程式を解くため，このように発生力などを扱う際には，ヤコビ行列を使った変換は一切必要ない．

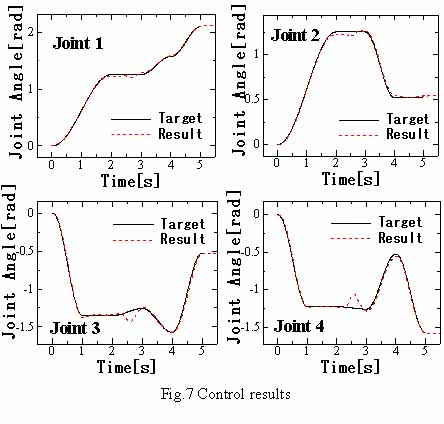
フィードフォワード制御とPIDフィードバック制御を組み合わせて適用した場合の，各関節角の追従結果を図7に示す．2s～3sの間で軌道からのズレが見られるが，これは前述のように，拘束機構による連結時にスムーズに動作させることを目的とし，系内に力を発生させているためである．実験結果から，形態が変化するリンク系に対しても適切なトルク値が連続的に算出され，良好な軌道追従性を示すことが確認された．なお，フィードバック制御のみで実験を行った場合には，拘束動作を実現することができなかった．

4. 結言

本報告では，FEMを用いた並列的逆動力学計算法をフィードフォワード制御系に組み込み，その動作確認をした．本解法は，力の次元の運動方程式を増分的に解く近似解法であるが，制御過程中の計算時間は実用上十分に短いことが示された．さらに，形態が連続的に変化するリンク機構の制御に適用した結果，境界条件の変化に対応したトルク値が算出され，フィードフォワード制御系として十分に機能することが確認された．今後は，部材剛性の考慮によるフレキシブルマニピュレータへの適用，力の次元で方程式を扱う利点を生かした力制御への適用などを予定している．

参考文献

[1] 中村仁彦:“パラレルメカニズムの動力学”，日本ロボット学会誌, Vol.10, No.6, pp.709-714, 1992.

[2] 杉本浩一:“閉ループ機構の運動方程式の導出”,日本ロボット学会誌, Vol.14, No.3, pp.460-467, 1997.

[3] 磯部大吾郎: “有限要素法を用いたリンク機構の逆動力学計算”,日本ロボット学会誌, Vol.20, No.6, pp.647-653, 2002.